Analysis of Categorical Data
Analysis of Categorical DataIntroduction to categorical dataChi-Square TestsChi-square Goodness of Fit (GoF) testChi-square tests of independence
Introduction to categorical data
Many experiments result in measurements that are qualitative (categorical) rather than quantitative (numbers).
Example
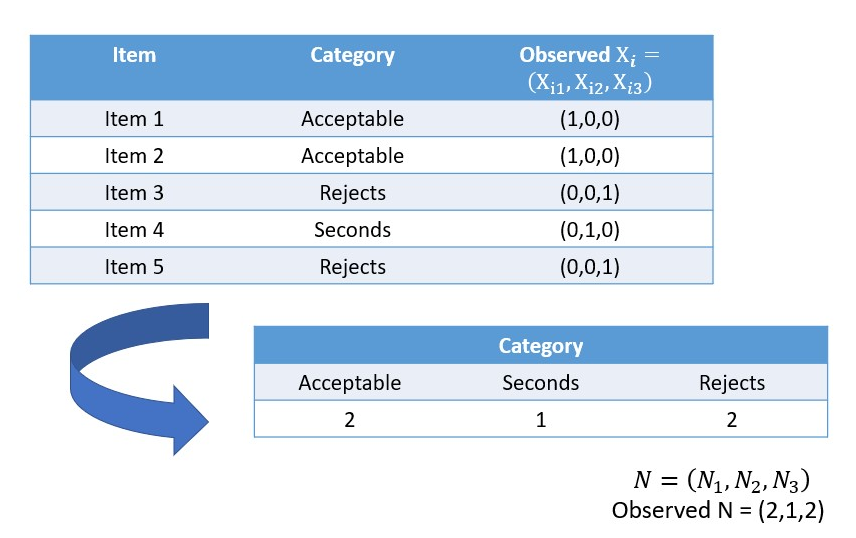
- manufactured items are sampled and categorized into "acceptable", "seconds", or "rejects"
- employees are surveyed and classified into one of five income brackets.
We can represent each outcome as a length- vector such that if belongs to the th category and otherwise for .
Note the sample can be summarized by providing the counts of the number of measurements that fall into each of the categories, i.e., by the random vector such that .
Definition (multinomial distribution) Consider a random experiment such that
- the experiment consists of independent and identical trials, and
- the outcome of each trial falls into exactly one of distinct categories.
Then the counts for each category () follow a multinomial distribution with the number of trials and cell probabilities (), i.e. .
The pmf for is
where the cell probabilities sum up to , i.e.,
Remark 1: a Binomial distribution is a special case of the multinomial distribution when , i.e., .
Remark 2: Suppose are i.i.d., such that . Then .
Using observed counts (i.e., a realization of ), we would like to make inferences about the category probabilities .
Chi-Square Tests
Setting
We have a random sample where each . Equivalently, we have a random variable such that .
- Null and alternative hypothesis:
at least one differs from the hypothesized value , ,
where are pre-specified probabilities such that .
- Test statistic:
Null distribution:
Given a significance level , the rejection region for the observed test statistic : , where the observed test statistic .
The test of "rejecting if the observed test statistic exceeds " is an approximate sig. level test.
Remark 1: this is an asymptotic test. The sample size needs to be large to approximate the null distribution with the distribution. A rule of thumb is to check whether for . In practice, we check whether each observed count exceeds or not.
Remark 2: this test has a connection with the asymptotic LRT. In fact, it can be shown that when is large. In particular, the degrees of freedom of the distribution is the difference of the number of free parameters in the null and full parameter spaces.
- Number of free parameters in the null parameter space =
- Number of free parameters in the full parameter space = .
Example: A group of rats, one by one, proceed down a ramp to one of three doors. We wish to test the hypothesis that the rats have no preference concerning the choice of a door. Suppose that the rats were sent down the ramp times and that the three observed cell frequencies were , and .
Chi-square Goodness of Fit (GoF) test
The test above can be used to test whether sample data are from a given distribution or not.
Idea: partition the range of into distinct regions () and compare observed and expected counts for each region.
- : vs.
- vs. : at least one differs from the hypothesized probability , where .
Example Let denote the number of heads that occur when four identical coins are tossed at random. Under the assumption that the four coins are independent and the probability of heads on each coin is , is . One hundred repetitions of this experiment resulted in , and heads being observed on , and trials, respectively. Do these results support the assumptions? Make a conclusion at .
Often, we are interested in testing whether the random variable of interest is from a certain family of distributions or not. Note, in such case, the distribution of is not completely specified under .
- Null and alternative hypotheses
- : vs.
- vs. : at least one differs from the hypothesized probability , where .
- Test statistic:
where is a ML estimator of under (i.e., ).
Null distribution:
where is the length of (i.e., the number of free parameters under ).
Given a significance level , the rejection region for the observed test statistic : , where the observed test statistic .
The test of "rejecting if the observed test statistic exceeds " is an approximate sig. level test.
Example The number of accidents per week at an intersection was checked for weeks; Out of weeks, weeks had no accidents, weeks had one accident, and weeks had accidents. Test the hypothesis that the random variable has a Poisson distribution, assuming the observations to be independent. Use .
Chi-square tests of independence
Two-way contingency table (a table for two categorical variables)
Example:
A statistics 415 instructor wants to know if there is a relationship between favorite color (red or yellow) and the preferred condiment on a corn dog. The following table summarizes the results.
| Condiment | |||
|---|---|---|---|
| Color | Ketchup | Mustard | Total |
| Red | |||
| Yellow | |||
| Total |
A general example of our contingency table with two classifying factors can be displayed as follows.
- denotes the count in the cell, i.e., the count in row and column . We use to denote the marginal total count for the th row, and the marginal total count for the jth column, and the overall total count, which is equal to , the sample size.
- When we talk about an contingency table, we mean a table with categories for the row variable and categories for the column variable
| Total | |||||
|---|---|---|---|---|---|
| Total |
In some problems, the counts , , can be modeled using a multinomial distribution
Assume each of the observations results in an outcome that can be classified by two attributes
- e.g, "Treatment/Control" on the rows, "Disease/No disease" on the columns
The first attribute is randomly assigned to one and only one of mutually exclusive and exhaustive events and the second attribute falls into one and only one the mutually exclusive events
Define
Chi-square tests of independence
Chi-square tests of independence aim to answer the question: for a single observation, is the row assignment statistically independent of the column assignment?
- In terms of hypotheses, we will test
, ,
vs.
for at least 1 pair.
Defining
we can rewrite and as
, ,
for at least 1 pair
- Test statistic:
where
the observed value at cell :
- the expected value at cell :
- Under , follows a distribution with degrees of freedom-that is, .
- the number of free parameters in the null parameter space:
- the number of free parameters in the full parameter space:
- the difference in the number of free parameters:
- Given a significance level , the rejection region for the observed test statistic : .
- Large discrepancy between observed and expected counts = favors the alternative hypothesis
Example:
Test whether there is a relationship between favorite color (red or yellow) and the preferred condiment on a corn dog at .
| Condiment | |||
|---|---|---|---|
| Color | Ketchup | Mustard | Total |
| Red | |||
| Yellow | |||
| Total |